Haydee Avila: 3.10 TEOREMA DE CONVOLUCION

establece que bajo determinadas circunstancias, la Transformada de Fourier de unaconvolución es el producto punto a punto de las transformadas. En otras palabras, la convolución en un dominio (por ejemplo el dominio temporal) es equivalente al producto punto a punto en el otro dominio (es decir dominio espectral).

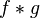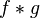Sean $f$ y $g$ dos funciones cuya convolución se expresa con $f \ast g$ . (notar que el asterisco denota convolución en este contexto, y no multiplicación; a veces es utilizado también el símbolo $\otimes$ ). Sea $\mathcal{F}$ el operador de la transformada de Fourier, con lo que $\mathcal{F}[f]$ y $\mathcal{F}[g]$ son las transformadas de Fourier de f y g, respectivamente.